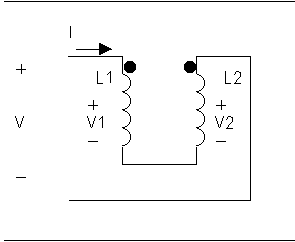
Figure 1 (a) |
Figure 1 (b) |
Date: 1/5/97
To: Rebecca Wang, EE 275 Graduate Teaching Assistant Department of Electrical Engineering
From: Randy Dimmett EE 275 A2 Laboratory
Subject: Mutual Inductance and Capacitance
Appendix I - Inductors
Appendix II - Capacitors
In this lab, mutual inductance and capacitance was studied. For studying inductance, two inductors were placed near to each other and two configurations were used to determine the equivalent inductance. One configuration caused the equivalent to be less, and the other configuration caused a greater inductance. For studying mutual capacitance, two copper pipes and a plate of aluminum were used. All three were put together closely, and the capacitance of each was measured. The purpose of doing this experiment is to show that a mutual inductance and a mutual capacitance exists between two inductive or capacitive elements when placed close to each other.
The dots on the inductors simply correspond to the positive end of a voltage drop. Physically, a magnetic field that is changing with respect to time will produce a current that will also have a magnetic field that will add or take from the original field. The dots help decide which way the current produced will flow. In figure 1(a) (Appendix 1), the dots correspond to the voltages v1 and v2, but in figure 2(b), v2 is actually labeled opposite of what it actually is (because the + end is not by the dot). Note that there is always a voltage drop across a passive component (such as an inductor). The inductor with the greater loop area has the greatest inductance because by definition, the inductance is directly proportional to the loop area. In other words, the greater the loop area, the greater the inductance.
Mutual Inductance and Capacitance (Continued)
In this experiment it was observed that the greater separation between the capacitors, the less the capacitance was. This is because again, by definition, the capacitance is inversely proportional to the distance between the capacitor's plates (which in this experiment was the pipes and aluminum plate). Also, by the definition of capacitance, it is important that the capacitor's materials have the potential for being capacitive. The self-capacitance as well as the mutual capacitance created both depend on the capacitive potential of the material
Appendix I - Inductors
Mutual Inductance and Capacitance

Figure 1 (a) |
Figure 1 (b) |
Leqa: 47.3 mH
Leqb: 104.9 mH
LCR Frequency setting: 1 kHz
|
L1 Designation: #1 |
L2 Designation: #2 |
From Preliminary:
(1) Leqa=L1+L2-2M
(2) Leqb=L1+L2+2M
Max{ Leqa, Leqb} = Leqb = L1+L2+2M Which implies that 2M
= Max{ Leqa, Leqb}-L1-L2
Therefore, M = (Max{ Leqa, Leqb}-L1-L2) / 2 = 14.1 mH %
Min{ Leqa, Leqb} = Leqa = L1+L2-2M Which implies that 2M
= -Max{ Leqa, Leqb}+L1+L2
Therefore, M = -(Min{ Leqa, Leqb}-L1-L2) / 2 = 14.7 mH %
Difference: 100% * | 14.1 - 14.7 | / 14.7 = 4.08 %
Appendix II - Capacitors
Mutual Inductance and Capacitance
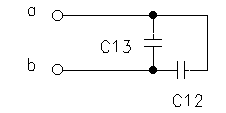
figure 2 (a) |
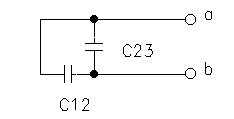
figure 2 (b) |
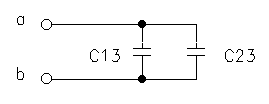
figure 2 (c) |
Results from preliminary:
(1) C1 = C13 + C12
(2) C2 = C23 + C12
(3) C3 = C13 + C23
(C1+C2 - C3)/2 = [(C13 + C12) + ( C23 + C12) - (C13 + C23)] / 2 = 2* C12 / 2 = C12
(C2+C3 - C1)/2 = [(C23 + C12) + (C13 + C23) - (C13 + C12)] / 2 = 2* C23 / 2 = C23
(C1+C3 - C2)/2 = [(C13 + C12) + (C13 + C23) - (C23 + C12)] / 2 = 2* C13 / 2 = C13
Using one sheet of paper:
Ca (C-1 with #2 and #3 shorted): 140.0 pf
Cb (C-2 with #1 and #3 shorted): 144.0 pf
Cc (C-3 with #1 and #2 shorted): 219 pf
C12 = 32.5 pf
C23 = 111.5 pf
C13 = 107.5 pf
Using two sheets of paper:
Ca (C-1 with #2 and #3 shorted): 121.5 pf
Cb (C-2 with #1 and #3 shorted): 126.4 pf
Cc (C-3 with #1 and #2 shorted): 187 pf
C12 = 30.45 pf
C23 = 95.95 pf
C13 = 91.05 pf